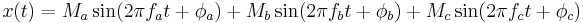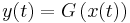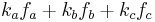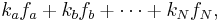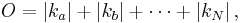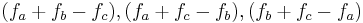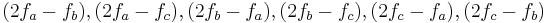Intermodulation
Intermodulation or intermodulation distortion (IMD) is the amplitude modulation of signals containing two or more different frequencies in a system with nonlinearities. The intermodulation between each frequency component will form additional signals at frequencies that are not just at harmonic frequencies (integer multiples) of either, but also at the sum and difference frequencies of the original frequencies and at multiples of those sum and difference frequencies.
Intermodulation is caused by non-linear behaviour of the signal processing being used. The theoretical outcome of these non-linearities can be calculated by generating a Volterra series of the characteristic, while the usual approximation of those non-linearities is obtained by generating a Taylor series.
Intermodulation is rarely desirable in radio or audio processing, as it creates unwanted spurious emissions, often in the form of sidebands. For radio transmissions this increases the occupied bandwidth, leading to adjacent channel interference, which can reduce audio clarity or increase spectrum usage. It should not be confused with harmonic distortion (which does have widespread use in audio effects processing), nor with intentional modulation (such as a frequency mixer in superheterodyne receivers) where signals to be modulated are presented to an intentional nonlinear element (multiplied) (see non-linear mixers such as mixer diodes and even single-transistor oscillator-mixer circuits). In audio, the intermodulation products are nonharmonically related to the input frequencies and therefore "off-key" with respect to the common Western musical scale.
Contents |
Causes of intermodulation
A linear system cannot produce intermodulation. If the input of a linear time-invariant system is a signal of a single frequency, then the output is a signal of the same frequency; only the amplitude and phase can differ from the input signal. However, non-linear systems generate harmonics, meaning that if the input of a non-linear system is a signal of a single frequency, 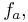 then the output is a signal which includes a number of integer multiples of the input frequency; (i.e some of
then the output is a signal which includes a number of integer multiples of the input frequency; (i.e some of 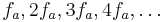 ).
).
Intermodulation occurs when the input to a non-linear system is composed of two or more frequencies. Consider an input signal that contains three frequency components at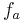 ,
, 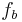 , and
, and 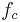 ; which may be expressed as
; which may be expressed as
where the 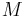 and
and 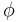 are the amplitudes and phases of the three components, respectively.
are the amplitudes and phases of the three components, respectively.
We obtain our output signal, 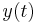 , by passing our input through a non-linear function:
, by passing our input through a non-linear function:
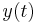 will contain the three frequencies of the input signal,
will contain the three frequencies of the input signal, 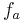 ,
, 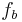 , and
, and 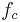 (which are known as the fundamental frequencies), as well as a number of linear combinations of the fundamental frequencies, each of the form
(which are known as the fundamental frequencies), as well as a number of linear combinations of the fundamental frequencies, each of the form
where 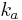 ,
, 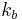 , and
, and 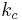 are arbitrary integers which can assume positive or negative values. These are the intermodulation products (or IMPs).
are arbitrary integers which can assume positive or negative values. These are the intermodulation products (or IMPs).
In general, each of these frequency components will have a different amplitude and phase, which depends on the specific non-linear function being used, and also on the amplitudes and phases of the original input components.
More generally, given an input signal containing an arbitrary number  of frequency components
of frequency components 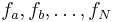 , the output signal will contain a number of frequency components, each of which may be described by
, the output signal will contain a number of frequency components, each of which may be described by
where the coefficients 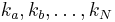 are arbitrary integer values.
are arbitrary integer values.
Intermodulation order
The order 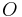 of a given intermodulation product is the sum of the absolute values of the coefficients,
of a given intermodulation product is the sum of the absolute values of the coefficients,
For example, in our original example above, third-order intermodulation products (IMPs) occur where 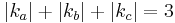 :
:
In many radio and audio applications, odd-order IMPs are of most interest, as they fall within the vicinity of the original frequency components, and may therefore interfere with the desired behaviour.
Passive intermodulation
As explained in a previous section, intermodulation can only occur in non-linear systems. Non-linear systems are generally composed of active components, meaning that the components must be biased with an external power source which is not the input signal (i.e. the active components must be "turned on"). However, even passive components can perform in a non-linear manner and cause intermodulation. Diodes are widely known for their passive nonlinear effects, but parasitic nonlinearity can arise in other components as well. For example, audio transformers exhibit non-linear behavior near their saturation point, electrolytic capacitors can start to behave as rectifiers under large-signal conditions, and RF connectors and antennas can exhibit non-linear characteristics. Even the air itself can behave in a non-linear fashion, which can be exploited to produce audible sound from intermodulation of ultrasonic frequencies.
Passive intermodulation (PIM) occurs in passive devices (which may include cables, antennas etc.) that are subjected to two or more high power tones. The PIM product is the result of the two (or more) high power tones mixing at device nonlinearities such as junctions of dis-similar metals, metal-oxide junctions and even loose connectors. The higher the signal amplitudes, the more pronounced the effect of the nonlinearities, and the more prominent the intermodulation that occurs - even though upon initial inspection, the system would appear to be linear and unable to generate intermodulation.
PIM can also occur in connectors, or when conductors made of two galvanically unmatched metals come in contact with each other. However, the most common source of passive intermodulation in connectors comes from the conduction of signal current through ferromagnetic metals such as nickel, which has a nonlinear magnetization-inductance hysteresis. This effect has been exploited to make reliable sources of PIM,[1] which can be used to cancel unwanted PIM from a system.[2]
Intermodulation in electronic circuits
Intermodulation is caused by nonlinearity or parameter limitations in an amplifier system. This nonlinearity can be characterized in many ways, including the slew rate, crossover distortion, reduced transistor current gain, or saturation of collector-emitter junctions near clipping. Slew-induced distortion (SID) can produce intermodulation distortion (IMD) when the first signal is slewing (changing voltage) at the limit of the amplifier's power bandwidth product. This induces an effective reduction in gain, partially amplitude-modulating the second signal. If SID only occurs for a portion of the signal, it is called "transient" intermodulation distortion.[3] This usually occurs due to soft clipping of the signal peaks.[4]
Intermodulation in audio applications
Audio engineers usually strive to avoid intermodulation, as for anything other than extremely simple input waveforms, it introduces frequency components that are not harmonically related, which tends to sound unmusical and unpleasant. However, certain audio effects rely on amplitude modulation; these include tremolo and ring modulation. One way to generate such effects is through deliberate intermodulation in a non-linear device, but may also be achieved without intermodulation by an analog multiplier. Transient intermodulation distortion, or TIM, occurs in amplifiers that employ negative feedback when signal delays make the amplifier incapable of correcting distortion when exposed to fast, transient signals.
Harmonic distortion occurs when non-linearity (in an amplifier or loudspeaker, for instance) only creates new frequencies that are harmonically related to the original signal. Intermodulation distortion occurs when a different type of non-linearity can create new frequencies that are not harmonically related to the original signal. All audio devices give rise to distortion to some extent; harmonic distortion and intermodulaton distortion tests highlight different aspects of imperfections, and one type of distortion may be inaudibly low while the other is significantly high for some equipment under certain conditions.
In analog recording, wow and flutter are forms of intermodulation distortion caused by speed variations in the medium (usually tape). When the flutter rate is above a certain point, typically about 20Hz, the modulation products impressed into the musical signal no longer present as an audibly obvious flutter, yet continue to interfere with the signal as extraneous frequency modulation, and the resulting sideband products manifest as distortion. This distortion results in a thicker, grainier texture due to the excess non-musical sum and difference components riding above and below the harmonic content of the material. Dewow and deflutter techniques such as those by Plangent Processes effectively minimize this distortion.
Measurement
Intermodulation distortion in audio is usually specified as the Root Mean Square (RMS) value of the various sum-and-difference signals as a percentage of the original signal's RMS voltage, although it may be specified in terms of individual component strengths, in decibels, as is common with RF work. Audio IMD standard tests include SMPTE standard RP120-1994 [3] where two signals (at 60 Hz and 7 kHz, with 4:1 amplitude ratios) are used for the test; many other standards (such as DIN, CCIF) use other frequencies and amplitude ratios. Opinion varies over the ideal ratio of test frequencies (e.g. 3:4,[5] or almost -but not exactly - 3:1 for example).
After feeding the equipment under test with low distortion input sinewaves, the output distortion can be measured by using a electronic filter to remove the original frequencies, or spectral analysis may be made using Fourier Transformations in software or a dedicated spectrum analyser, or when determining intermodulation effects in communications equipment, may be made using the receiver under test itself.
Using modern a network analyzer with two internal RF sources and sensitive RF detectors simplifies the measurement setup and also provides a sensitivity level comparable to spectrum analyzers. Furthermore, a calibrated VNA setup also removes mismatch errors from measurements which otherwise would be present in spectrum analyzer measurements. Meanwhile error-corrected IM measurement systems are available. These system support frequency converting vector-measurements of S-parameters.[6] The user can locate IM-sources and perform a vector or time-domain fitting or modelling of the IM-signals and components.
See also
- Rusty bolt effect
- Beat (acoustics)
- Audio system measurements
- Second-order intercept point
- Third-order intercept point, a metric of an amplifier or system related to intermodulation
External links
References
- ^ Henrie, J., Christianson, A. and Chappell, W. Engineered passive nonlinearities for broadband passive intermodulation distortion mitigation, Microwave and Wireless Components Letters, Vol. 19, pp.614-616, 2009. Available online.
- ^ Henrie, J., Christianson, A. and Chappell, W. Cancellation of passive intermodulation distortion in microwave networks, in European Microwave Conference, Amsterdam, The Netherlands, IEEE, 2008. Available online.
- ^ a b Rane Pro Audio Reference for IM
- ^ http://waltjung.org/PDFs/SID_TIM_TAA77_P1.pdf Slewing Induced Distortion in Audio Amplifiers, Part 1 by Walter Jung in The Audio Amateur Issue 1/1977
- ^ http://www.leonaudio.com.au/3-4.ratio.distortion.measurement.pdf Graeme John Cohen: 3-4 Ratio; A method of measuring distortion products
- ^ Thalayasingam, K. and Heuermann, H., Novel Vector Non-Linear Measurement System for Intermodulation Measurements, European Microwave Conference, Rom, Italy, IEEE, 2009, Available online
This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C" (in support of MIL-STD-188).